 zad1 Oblicz x wiedząc że tga = 3x tgb=3−x oraz a − b = pi/6
zad2 z punku O odległego od płaszczyzny pi o 5,5√2 poprowadzono dwie proste prostopadłe
nachylone do płaszczyzny pod kątem 30 stopni i przecinające ją w punktach M i N. Oblicz
długość odcinka MN
zad1 Oblicz x wiedząc że tga = 3x tgb=3−x oraz a − b = pi/6
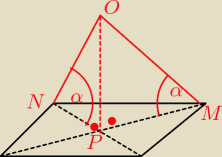
zad2 z punku O odległego od płaszczyzny pi o 5,5√2 poprowadzono dwie proste prostopadłe
nachylone do płaszczyzny pod kątem 30 stopni i przecinające ją w punktach M i N. Oblicz
długość odcinka MN
| √3 | ||
tg(a−b) = tgπ6 = | ||
| 3 |
| tga−tgb | 3x−3−x | |||
tg(a−b) = | = | = | ||
| 1+tga*tgb | 1+3x*3−x |
|
| |||||||||||||||||
= | = | |||||||||||||||||
| 1+3x−x | 1+30 |
| 32x−1 | ||||||||
= | |||||||||
| 2 | 2*3x |
| 32x−1 | √3 | 31/2 | |||
= | = | = 3−1/2 | |||
| 2*3x | 3 | 31 |
| 4 | 16 | |||
Δ=4*3−1−4*1*(−1) = | +4 = | |||
| 3 | 3 |
| 4 | ||
√Δ = | ||
| √3 |
| 2 | 4 | −2 | −1 | |||||
t1 = U{ | − | {2} = | = | <0 | ||||
| √3 | √3 | 2√3 | √3 |
| 2 | 4 | 6 | 3 | |||||
t2 = U{ | + | {2} = | = | =√3>0 | ||||
| √3 | √3 | 2√3 | √3 |

| 11 | ||
OP= | √2 | |
| 2 |
| 121 | ||
(2x)2=x2+ | *2 | |
| 4 |
| 121 | ||
4x2−x2 = | ||
| 2 |
| 121 | ||
3x2= | ||
| 2 |
| 121 | ||
x2 = | ||
| 6 |
| 11 | ||
x = | ||
| √6 |
| 11 | 22 | |||
ON=OM = 2* | = | |||
| √6 | √6 |
| 22 | 22 | 22√3 | ||||
MN = ON√2 = | *√2 = | = | ||||
| √6 | √3 | 3 |

